| Quelle | Lindemann et al. „The application of the Multiple-Domain Matrix: Considering multiple domains and dependency types in complex product design.“ Systems, Man and Cybernetics, 2008. SMC 2008. IEEE International Conference on. IEEE, 2008. |
|---|---|
| Einsatz | Produktentwicklung. Kann auch für Dienstleistungen eingesetzt werden, z. B. Versorgungsnetzwerk zur Behandlung von Depressionen. |
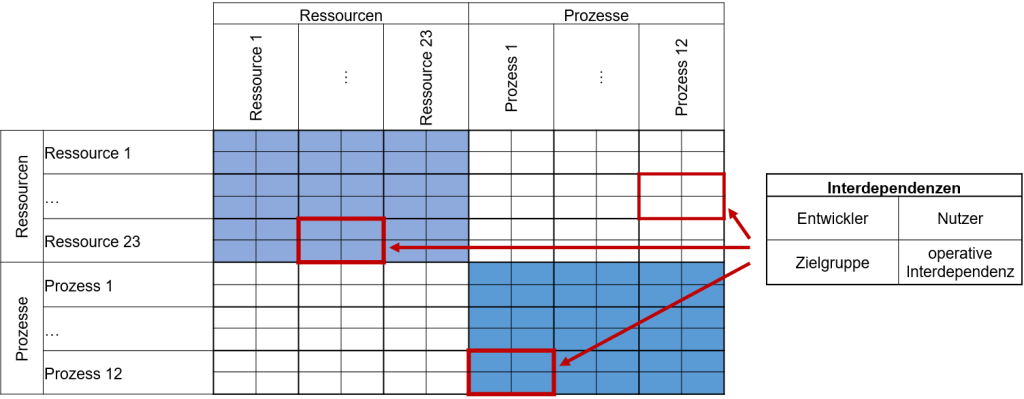
| Idee | MDM ist eine Erweiterung von DSM, bei der verschiedene Domänen integriert werden. MDM besteht aus einer beliebigen Anzahl von DSM (Beschreibung der Elemente einer Domäne, also n * n) und DMM (Domain mapping matrix: setzt die Elemente von zwei verschiedenen Domänen miteinander in Beziehung, also n*m) zusammensetzt. Z. B. bei 2 Domänen (Prozessen und Ressourcen) werden insgesamt 4 Matrizen gebildet:
Bei Bedarf können einzelne Beziehungen weiter aufgeteilt werden, z. B. nach Zielgruppe |
| Phasen im Modularisierungsablauf | Strukturierung |
| Modulstruktur | Komplexe Struktur |
| Input | Dienstleistung, die in einzelne Komponente (und das für mehrere Dimensionen, z. B. Prozesse und benötigte Ressourcen) bereits zerlegt wurde |
| Output | Abhängigkeitsmatrix, die die (mehrdimensionale) Interdependenzen und ihre Stärken beinhaltet. |
| Anwendungs- voraussetzung |
Ähnlich wie bei DSM, braucht MDM bereits eine dekomponierte Dienstleistung. Der Vorteil der MDM ist die mehrdimensionale Darstellung, sodass eine simultane Optimierung über mehrere Dimensionen möglich wird. Auch hier werden weitere Cluster-Algorithmen zur Modulbildung benötigt. In dem Beitrag von Dörbecker et al. (2013) wird der Schritt der Modulbildung jedoch nicht näher erläutert, sodass keine Angaben über die Komplexität dieses Schrittes gemacht werden können |
| Vorgehen |
|
| Fazit | Vorteil: Mehrdimensionale Sichtweise auf die Interdependenzen, somit mehr Informationsgehalt als bei DSM. Nachteil: Für die Auswertung dieser Matrizen und die eigentliche Modulbildung werden adäquate algorithmische Verfahren benötigt (Clusterverfahren), deren Komplexitätmit der steigenden Anzahl von Dimensionen überproportional ansteigen wird (bei 3 Dimensionen wären es bpsw. schon 9 Matrizen). |