| Quelle | Ho H. C., Haung C. C., Yang H. L. Development of Modular Services //New Trends in Information and Service Science, 2009. NISS’09. International Conference С. 1215-1220. |
|---|---|
| Einsatz | Ursprünglich für die Modularisierung von Software Services entwickelt, aber auch an Flughafenabläufen getestet. Andere Felder sind allerdings auch vorstellbar, da die Methode nicht an bestimmte Anwendungskontexte/Prozesse gebunden ist. |
| Idee | Wenn ein Service einen anderen Service „aufruft“, entsteht dabei eine Interaktion. Ein System bzw. Programm kann demnach als Graph repräsentiert werden, in dem einzelne Services als Knoten und ihre „Aufrufe“ als Kanten dargestellt sind. Die Interaktion kann durch die Kupplung (Coupling), also die Stärke der Verbindung zwischen den Modulen, und den Zusammenhang (Cohesion), also die Stärke der Verbindung der Dienstleistungen innerhalb eines Moduls, beschrieben werden. Es wird demnach versucht, die Software in solche Module zu teilen, sodass die inter-modale Interaktion minimiert (low coupling) und intra-modale Beziehungen maximiert (high cohesion) werden. Dadurch lässt sich verhindern, dass ein Fehler im Modul sich auf andere Module verbreitet. Die Basis für den Algorithmus bildet der Interaction Graph (A, E, W), wobei A = Menge der Services, E = Menge der Interaktionen zwischen den Services, und W Menge der Gewichtungen bzw. Häufigkeit der Aufrufe ist. Zusätzlich wird ein Qualitätsmerkmal eines Clusters eingeführt – “Gewichtungsdichte” (weight density), die als das Verhältnis von der Summe der Gewichtungen von Cohesion-Kanten im Sub-Graph über die Anzahl der Cohesion-Kanten gebildet wird. 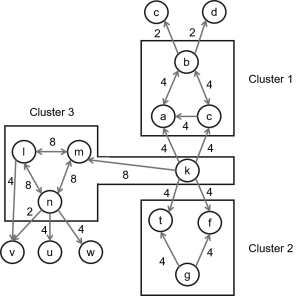 |
| Phasen im Modularisierungsablauf | Strukturierung → Modulbildung |
| Modulstruktur | Logische Struktur (Stückliste) |
| Input | Zerlegte Dienstleistung und die Abhängigkeit einzelner Komponente miteinander. |
| Output | Fertige Module. Falls ein Interaction Graph mitgezeichnet wird, dann auch die Visualisierung des Ergebnisses und die Möglichkeit zur weiteren Konfiguration. |
| Anwendungs- voraussetzung |
Die Voraussetzung für die Anwendung des Algorithmus ist ein vollständig ausgefüllter Interaction Graph. Zudem müssen die Anwender angeben, wie viele Module gewünscht sind (Nu) und wie groß der Grenzindex (Θ) sein darf. Je höher Θ gesetzt wird, desto strikter sind die Anforderungen an die Modulbildung, sprich weniger Knoten in einem Modul bzw. mehr Module. |
| Vorgehen | 0. (Initialisierung): Definiere die maximal zugelassene Anzahl von Modulen (NU) und lege den Grenzindex (Θ) fest.
1. (Labeling): Wähle die nicht-markierte Kanten mit dem gleichen größten Gewicht und markiere diese (=lösche sie aus der Menge). 2. (Clustering): Identifiziere die verbundene Sub-Graphs mit den neuen markierten Kanten. Füge die jeweiligen Knoten des Sub-Graphs in einen Cluster solange die Nebenbedingungen (siehe angegebene Quelle) nicht verletzt werden. 3. (Identifizierung): Identifiziere die Module, die den Clustern im Graph entsprechen. 4. (Klassifizierung): Klassifiziere die generierten Module auf Basis von Eigenschaften (siehe angegebene Quelle). 5. (Terminierung): Abbruch und Ausgabe des Ergebnisses. |
| Fazit | Vorteil: Da der Algorithmus zahlenbasiert ist und das Ergebnis von solchen Angaben wie Threshold Index (Θ) oder maximale Anzahl der Module (NU) abhängt, können verschiedene Szenarien recht einfach computergestützt simuliert werden. Nachteil: Der Ursprungsgedanke des Algorithmus kommt aus dem Bereich der Software Entwicklung, wo einzelne Services sich mehrmals aufrufen (z. B. achtmal), was für die Berechnung der Gewichtungsdichte benötigt wird. Inwieweit dies auf Dienstleistungen im Allgemeinen anwendbar ist, ist unklar. Des Weiteren beschäftigt sich der Algorithmus ausschließlich mit dem Schritt der Modulbildung und setzt eine dekomponierte Dienstleistung voraus. |